ควอนตัมเทเลพอเทชัน (Quantum teleportation) -

สวัสดีครับ วันนี้ทางเพจ QuTE จะพาไปทำความเข้าใจหลักการทำงานพื้นฐานของควอนตัมเทเลพอเตชัน(Quantum teleportation)โดยอาศัยสมบัติทางควอนตัมระหว่าง 2 อนุภาคที่เรียกว่า ควอนตัมเอนแทงเกิลเมนต์ (Quantum entanglement)

หลายคนเมื่อได้ยินคำว่าเทเลพอเตชันแล้วจะนึกไปถึงภาพยนต์แนววิทยาศาสตร์หลายๆเรื่อง เช่น Star Trek ที่มีการเทเลพอร์ตคนจากยานอวกาศลงไปยังดาว ซึ่งรูปแบบในภาพยนต์นั้นมีการส่งมวลสารและข้อมูลจากต้นทางไปประกอบกันขึ้นมาเป็นคนใหม่ที่ปลายทาง(คิดๆดูหากเครื่องเทเลพอร์ตนั้นเกิดผิดพลาดขึ้นมา เอาแขนไปต่อขา เอาขาไปหูงี้ น่าจะแย่นะครับ ฮาาา)

ในความเป็น(ตามหลักฟิสิกส์) นั้นสิ่งที่เราสามารถส่งไปยังปลายทางได้(หรือเทเลพอร์ต)คือ สถานะซึ่งในที่นี้คือสถานะควอนตัม แนวคิดควอนตัมเทเลพอเตชันนั้นได้ถูกเสนอโดยกลุ่มนักฟิสิกส์ตามรูปด้านล่าง

ข้อมูลเพิ่มเติมดูได้ที่ https://researcher.watson.ibm.com/researcher/view_group.php?id=2862

แผนภาพกระการทำควอนตัมเทเลพอเตชันแสดงดังด้านล่างซึ่งหาได้ทั่วไปตามอินเตอร์เน็ต ซึ่งเมื่อเสร็จกระบวนการสถานะของอนุภาค C จะโดนโอนถ่ายไปให้อนุภาค B ซึ่งอยู่ ณ จุดหมายปลายทาง

http://universe-review.ca/R15-26-entangle.htm

เพื่อให้ง่ายต่อการทำความเข้าใจเราจะแบ่งขั้นตอนตามนี้

ขั้นตอนที่ 1

เราต้องเตรียมคู่อนุภาคที่แอนแทงเกิลกันอยู่สูงสุด(Maximally entangled state) ให้ชื่อว่า A และ B แล้วกันครับ จากนั้นก็แยกออกจากกัน A มอบให้กับอลิส ส่วน B มอบให้บ๊อบ โดยทั้ง 2 นั้นอยู่ที่ห้องปฏิบัติการคนละที่ เราอาจจะมองได้ว่าอนุภาค A และ B เป็นแฟนกัน

ขั้นตอนที่ 2

อลิสนำอนุภาคอีกตัวเข้ามา อาจจะเรียกว่า C โดยมีสถานะ ⏀ ซึ่งเป็นสถานะที่เราต้องการส่งไปให้บ๊อบที่อยู่อีกห้องปฏิบัติการ

ตรงนี้เราอาจมองได้ว่าอลิสนั้นได้นำเอามือที่ 3 คือ C เข้ามาในความสัมพันธ์ระหว่าง A และ B

ขั้นตอนที่ 3

อลิสดำเนินการแปลงสำหรับสถานะ A และ C ทำให้ C เข้าไปแทรกสภาวะแอนแทงเกิลระหว่าง A กับ B

ตรงนี้เรามองว่าอลิสนั้นส่งเสริมให้ A คบซ้อนกับ C ทั้งๆที่มี B อยู่แล้ว !!

ขั้นตอนที่ 4

จากนั้นอลิสทำการวัดสถานะ AC (joint measurement) และทำการสื่อการผลของการวัดกับบ๊อบ เมื่อบ๊อบรู้ผลของการวัดของอลิส เขาอาจจะทำการแปลงบางอย่างเพื่อให้สถานะ⏀ถูกส่งไปยัง B ออกมา หลังจากนั้น A และ C กลายเป็นคู่แอนแทงเกิลสูงสุดแทน

ตรงนี้เราอาจมองได้ว่ารักต้องเลือก หาก A เลือก C ก็ต้องตัด B คบซ้อนไม่ดี

คราวนี้เราลองมาดูขั้นตอนทางคณิตศาสตร์อย่างละเอียดกันนะครับว่ากระบวนการส่งสถานะควอนตัมนั้นทำอย่างไร

ขั้นตอนที่ 1

ทำให้สถานะควอนตัมระหว่างอนุภาค A และ B อยู่ในรูป

$|\Psi_{AB}^+>=\frac{1}{\sqrt 2}\left(|0_A>|0_B>+|1_A>|1_B> \right).................(1)$

ซึ่งเรียกว่าสถานะพัวพันทางควอนตัมระหว่าง 2 อนุภาคแบบสูงสุด สถานะในสมการ (1) นั้นรู้จักกันในชื่อสถาะเบลล์ (Bell states) โดยมีอยู่ด้วยกัน 4 แบบ อีก 3 แบบที่เหลือคือ

$|\Psi_{AB}^->=\frac{1}{\sqrt 2}\left(|0_A>|0_B>-|1_A>|1_B> \right).................(2)$

$|\Phi_{AB}^+>=\frac{1}{\sqrt 2}\left(|0_A>|1_B>+|1_A>|0_B> \right).................(3)$

$|\Phi_{AB}^->=\frac{1}{\sqrt 2}\left(|0_A>|1_B>-|1_A>|0_B> \right).................(4)$

ขั้นตอนที่ 2

อลิสนำเอาอนุภาค C มาซึ่งมีสถานะ $|\Phi_C>=a|0_C>+|1_C>$ โดนที่ $|a|^2+|b|^2=1$ ทำให้สถานะรวมของทั้งระบบตอนนี้เขียนได้เป็น

$|\Phi_C>|\Psi_{AB}^+>=\left(a|0_C>+|1_C>\right)\frac{1}{\sqrt 2}\left(|0_A>|0_B>+|1_A>|1_B> \right).................(5)$

เมื่อทำการกระจายจะได้

$|\Phi_C>|\Psi_{AB}^+>=\frac{a}{\sqrt 2}|0_C>|0_A>|0_B>-\frac{a}{\sqrt 2}|0_C>|1_A>|1_B>$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+\frac{b}{\sqrt 2}|1_C>|0_A>|0_B>-\frac{b}{\sqrt 2}|1_C>|1_A>|1_B>.................(6)$

ขั้นตอนที่ 3

จากนั้นจองดูสถานะระหว่าง C และ A และพบว่าสามารถแปลงอยู่ในรูปสถานะเบลล์ได้งานความสัมพันธ์

$|0>|0>=\frac{1}{\sqrt 2}\left( |\Psi^+>+|\Psi^->\right)\;\;\;\;\;\;\;\;\;\;|1>|1>=\frac{1}{\sqrt 2}\left( |\Psi^+>-|\Psi^->\right)$

$|0>|1>=\frac{1}{\sqrt 2}\left( |\Phi^+>+|\Phi^->\right)\;\;\;\;\;\;\;\;\;\;|1>|0>=\frac{1}{\sqrt 2}\left( |\Phi^+>-|\Phi^->\right)$

สมการ (6) เขียนใหม่เป็น

$|\Phi_C>|\Psi_{AB}^+>=\frac{1}{ 2}|\Psi_{AC}^+>(a|0_B>+b|1_B>)+\frac{1}{ 2}|\Psi_{AC}^->(a|0_B>-b|1_B>)$

$+\frac{1}{ 2}|\Phi_{AC}^+>(b|0_B>+a|1_B>)+\frac{1}{ 2}|\Phi_{AC}^->(b|0_B>-a|1_B>).................(7)$

(อลิสและบ๊อบรู้ขั้นตอนการแปลงทางคณิตศาสตร์ตรงนี้ด้วยกันทั้งคู่)

สมการด้านบนนั้นเราแค่ทำการเปลี่ยนการเขียนสถานะอนุภาค C และ A ซึ่งอยู่กับอลิศให้อยู่ในสถานะเบลล์เท่านั้นเอง โดยที่ยังไม่ได้ดำเนินการอะไรกับอนุภาคทั้งสาม การเคลื่อนย้ายสถานะควอนตัมยังไม่ได้เกิดขึ้น

ขั้นตอนที่ 4

การเคลื่อนย้ายสถานะควอนตัมเกิดขึ้นเมื่ออลิสทำการวัดสถานะอนุภาค C และ A ด้วยกัน (Joint measurement) ในเบสิสของเบลล์ ซึ่งจะเกิดการยุบตัวของฟังก์ชันคลื่น(จากที่อยู่ในสถานะซ้อนทับ)ให้ผลออกมาอย่างสุ่มเป็น 1 ใน 4 ของสถานะย่อย และทำการสื่อสารผลของการวัดของเธอกับบ๊อบ การวัดของอลิสนั้นทำให้ความสัมพันธ์ระหว่าง A ขาดลงกับ B แต่กลับไม่สร้างความสัมพันธ์กับ C แทน

กรณีที่ 1 หากอลิสวัดสถานะระหว่าง C และ A ได้เป็น $|\Psi_{AC}^+>$

เมื่ออลิสโทรไปบอกบ๊อบสถานะที่เธอวัดได้ ดังนั้นบ๊อบจะรู้ทันทีว่าสถานะของ B นั้นเป็นสถานะของ C ในตอนแรก เขาไม่ต้องทำอะไรต่อ ถือว่าการเคลื่อนย้ายสถานะควอนตัมสมบูรณ์

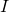แผนภาพแสดงการที่บ๊อบส่งสถานะเขาหลังจากที่สื่อสารกับอลิสเข้าไปยังควอนตัมเกต (Quantum gate) $I$ ซึ่งเท่ากับว่าไม่ได้ทำอะไร

กรณีที่ 2 หากอลิสวัดสถานะระหว่าง C และ A ได้เป็น $|\Psi_{AC}^->$

เมื่ออลิสโทรไปบอกบ๊อบว่าสถานะที่เธอวัดได้ ดังนั้นบ๊อบจะรู้ทันทีว่าสถานะของ C นั้นยังไม่อยู่ในสถานะของ A ในตอนเริ่มต้น (ผิดที่เครื่องหมายตรงกลาง) $a|0_B>-b|1_B>$ ดังนั้นบ๊อบต้องทำบางอย่าง สิ่งที่เข้าทำคือนำเอาสถานะดังกล่าวเข้าไปผ่านยูนิแทรี่เกต $\sigma_3$ ซึ่งจะทำให้ได้สถานะดังเดิมของ A ถือว่าการเเคลื่อนย้ายสถานะสมบูรณ์

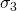แผนภาพแสดงการที่บ๊อบส่งสถานะเขาหลังจากที่สื่อสารกับอลิสเข้าไปยังควอนตัมเกต (Quantum gate) $\sigma_3$ ซึ่งจะทำการแปลงเครื่องหมายให้กลับมาถูก

กรณีที่ 3 หากอลิสวัดสถานะระหว่าง C และ A ได้เป็น $|\Phi_{AC}^+>$

เมื่ออลิสโทรไปบอกบ๊อบว่าสถานะที่เธอวัดได้ ดังนั้นบ๊อบจะรู้ทันทีว่าสถานะของ C นั้นยังไม่อยู่ในสถานะของ A ในตอนเริ่มต้น (ผิดที่เครื่องหมายตรงกลาง) $b|0_B>+a|1_B>$ ดังนั้นบ๊อบต้องทำบางอย่าง สิ่งที่เข้าทำคือนำเอาสถานะดังกล่าวเข้าไปผ่านยูนิแทรี่เกต $\sigma_1$ ซึ่งจะทำให้ได้สถานะดังเดิมของ A ถือว่าการเเคลื่อนย้ายสถานะสมบูรณ์

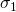แผนภาพแสดงการที่บ๊อบส่งสถานะเขาหลังจากที่สื่อสารกับอลิสเข้าไปยังควอนตัมเกต (Quantum gate) $\sigma_1$ ซึ่งจะทำการสลับสัมประสิทธิ์

กรณีที่ 4 หากอลิสวัดสถานะระหว่าง C และ A ได้เป็น $|\Phi_{AC}^->$

เมื่ออลิสโทรไปบอกบ๊อบว่าสถานะที่เธอวัดได้ ดังนั้นบ๊อบจะรู้ทันทีว่าสถานะของ C นั้นยังไม่อยู่ในสถานะของ A ในตอนเริ่มต้น (ผิดที่เครื่องหมายตรงกลาง) $b|0_B>-a|1_B>$ ดังนั้นบ๊อบต้องทำบางอย่าง สิ่งที่เข้าทำคือนำเอาสถานะดังกล่าวเข้าไปผ่านยูนิแทรี่เกต $-\sigma_3\sigma_1$ ซึ่งจะทำให้ได้สถานะดังเดิมของ A ถือว่าการเเคลื่อนย้ายสถานะสมบูรณ์

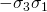แผนภาพแสดงการที่บ๊อบส่งสถานะเขาหลังจากที่สื่อสารกับอลิสเข้าไปยังควอนตัมเกต (Quantum gate) $-\sigma_3\sigma_1$ ซึ่งจะทำการสลับสัมประสิทธิ์และเครื่องหมายลบ

ข้อสังเกต 1 หลังจากสถานะของ C ถูกเคลื่อนย้ายไปยัง B แล้ว สถานะของ C จะเปลี่ยนไปเป็นสถานะคู่พัวพันกับ A ซึ่งแน่นอนว่าไม่ได้อยู่ในสถานะเดิม ซึ่งสอดคล้องกับทฤษฏีบทที่ว่า สถานะควอนตัมสำเนาไม่ได้ (No-cloning theorem) ซึ่งตรงนี้ต่างจากกรณีทีทำการเทเลพอร์ตแบบธรรมดา ดังนี้

พิจารณาสถานะการต่อไปนี้ สมมติอลิสมีกล่อง 4 เหลี่ยม เธอสามาถส่งสถานะ(ในที่นี้คือ กว้าง ยาว สูง) โดยการโทรไปบอกบ๊อบ ณ อีกห้องแลป ซึ่งบ๊อบต้องมีกระดาษเตรียมไว้รอสร้างกล่อง 4 เหลี่ยมอยู่แล้ว เมื่อเขารู้สถานะเขาก็แค่พับตาม สุดท้ายหลังจบกระบวนการเราจะมีกล่อง 2 กล่องที่เหมือนกัน คือตัวต้นฉบับและตัวที่สร้างใหม่

ขั้นตอนการเทเลพอร์ตสถานะสิ่งของแบบธรรมดา

คราวนี้เรามาดูสถานะทางควอนตัมบ้างครับว่าทำไมถึงทำเหมือนกันกรณีกล่องไม่ได้ ปกติสำหรับอลิสนั้นเธอสามารถพับกล่องที่เหมือนกันขึ้นมากี่อันก็ได้เท่าที่เธอต้องการ หรือถ้าเธอมีเอกสารเธอต้องการทำสำเนา เธอก็เอาไปเข้าเครื่องถ่ายเอกสาร จะเอากี่แผ่นก็กดไปว่างั้น ต้นฉบับเธอก็ยังอยู่ หากเราไม่คิดอะไรมาก สำหรับสถานะควอนตัมเราก็น่าจะทำได้เหมือนกันโดยอาศัยเครื่องถ่ายเอกสารควอนตัม(อะไรทำนองนั้น)

ขั้นตอนในการทำสำเนาสถานะควอนตัม(ซึ่งอยู่ในสถานะซ้อนทับของเบสิส $|1>$ และ $|0>$ ) เริ่มต้นเราต้องมีสถานะต้นแบบและสถานะเตรียมโดยถ่ายสำเนา $|0>$ (เทียบเหมือนกระดาษเปล่า) ซึ่งทั้งสองอยู่สถานะร่วม (Joint state) $|\Psi>|0>$ การที่จะทำให้เกิดการถ่ายสำเนาส่งไปยังสถานะเตรียมนั้นต้องมีตัวดำเนินการ (เทียบได้กับเครื่องถ่ายเอกสาร) $U$ ดังนี้

$U|\Psi>|0>=U|\Psi>|\Psi>.................(8)$

หากเราต้องการทำสำเนาเบสิส เราก็สามาถทำได้ผ่าน $U$ ดังนี้

$U|0>|0>=U|0>|0>.................(9)$

$U|1>|0>=U|1>|1>.................(10)$

ทุกอย่างดูเหมือนจะโอเคทุกอย่างเท่าทีผ่านมา โอเคคราวนี้ลองดูสถานะการณ์ต่อไปนี้ หากตอนนี้เรามีสถานะ 2 สถานะที่นิยามอยู่บนปริภูมิฮิลเบิร์ตเดียวกัน: $|\Psi>\in\mathcal H$ และ $|\Phi>\in\mathcal H$ ที่ต้องการทำสำเนาในแบบควอนตัม

$U|\Psi>|0>=U|\Psi>|\Psi>\;\;\;\;\;\;\;\;\;\;\;U|\Phi>|0>=U|\Phi>|\Phi>$

และผลคูณภายในของทั้ง 2 สถานะก่อนที่จะโดนทำสำเนาเป็น

$(<\Psi|<0|)(|0>|\Phi>)=<\Psi|<0|0>|\Phi>=<\Psi|\Phi>.................(11)$

เนื่องจาก $U$ เป็นตัวดำเนินการยูนิแทรี่ดังนั้น $U^\dagger U=I$ เราสามารถเติมเข้าไปตรงกลางของสมการด้านบน(พจน์ที่ 2)จะได้

$<\Psi|<0|U^\dagger U|0>|\Phi>=<\Psi|\Phi>.................(12)$

การด้านบนนั้นบอกให้เราทำการสำเนาสถานะไปทางซ้ายและทางขวา จะได้

$<\Psi|<\Psi||\Phi>|\Phi>=<\Psi|\Phi><\Psi|\Phi>=|<\Psi|\Phi>|^2.................(13)$

เนื่องจาก (11)=(13) จะให้เงื่อนไข

$<\Psi|\Phi>=|<\Psi|\Phi>|^2\rightarrow(<\Psi|\Phi>-1)<\Psi|\Phi>=0.................(14)$

สมการด้านบนเป็นจริงเมื่อ $<\Psi|\Phi>=0$ ซึ่งบอกว่าสถานะทั้ง 2 ตั้งฉากกัน และ $<\Psi|\Phi>=1$ ซึ่งบอกว่าสถานะทั้ง 2 ตั้งขนานกัน เห็นได้ชัดว่าผลที่ได้ขัดแย้งกันเอง ดังนั้นตัวดำเนินการ $U$ ไม่มีอยู่จริงสำหรับกระบวนการข้างต้น

ข้อสังเกตที่ 2 การที่อนุภาค A ตัดความสัมพันธ์เปลี่ยนคู่แอนแทงเกิลจาก B ไปเป็น C นั้นเป็นสมบัติที่เรียกว่า ควอนตัมโมโนกามี่ (Quantum monogamy) สำหรับคู่ที่อยู่ในสถานะแอนแทงเกิลสูงสุด จะไม่สามารถแบ่งใจไปสร้างความสัมพันธ์กับอนุภาคที่ 3 อีกได้ หากต้องการไปหาอนุภาคใหม่จริงๆ ก็ต้องตัดสัมพันธ์เก่าไปเลย (ฟังดูเหมือนชีวิตคน ^^)

https://www.youtube.com/watch?v=t07cXwpGZWI

ข้อสังเกตที่ 3 ควอนตัมเทเลพอเทชันไม่สามารถนำไปประยุกต์เพื่อการสื่อสารที่เร็วกว่าแสงได้ ประเด็นที่หลายๆคนอาจจะคิดว่าการสื่อสารที่เร็วกว่าแสงเกิดขึ้นได้เพราะสมบัติของคู่อนุภาคที่แอนแทงเกิลกัน เพราะทั้งสองอนุภาครับรู้ถึงการเปลี่ยนสถานะควอนตัมแบบทันทีทันใด ดังนั้นหากอลิสต้องการสื่อสารกับบ๊อบด้วยการส่งข้อมูลสถานะของ C ก็ดูเหมือนว่าจะทำได้ทันทีทันใด แต่จริงๆแล้วถึงแม้ว่าสถานะของ C จะถูกเคลื่อนย้ายไปยัง B แบบทันทีทันใด แต่ก็ยังต้องรอการสื่อสารระหว่างอลิสและบ๊อบผ่านช่องทางพูดคุยปกติอยู่ดี(ขั้นตอนที่ 4) ดังนั้นจึงไม่สามารถนำไปประยุกต์เพื่อการสื่อสารที่เร็วกว่าแสงได้

ข้อสังเกตที่ 4 ประเด็นสุดท้ายคือ อย่างที่ได้อธิบายไป เราทำการแค่เคลื่อนย้ายสถานะควอนตัมระหว่างสองตำแหน่งที่อาจจะอยู่ไกลกันมากๆ ไม่ได้ทำการเคลื่อนย้ายสสารหรือพลังงานเหมือนอย่างในภาพยนต์

ความน่าสนใจคือควอนตัมเทเลพอเตชันไม่ได้อยู่ในแค่ห้องแลปอีกต่อไป ในปี 2016 จีนสามารถส่งสถานะควอนตัมเป็นระยะทาง 1200 กิโลเมตร โดยผ่านดาวเทียมดังรูปประกอบ ซึ่งถือได้ว่าเป็นความสำเร็จแบบก้าวกระโดดในการสร้างเทคโนโลยีการสื่อสารแบบใหม่ในอนาคต ดูเพิ่มเติม

https://www.metabunk.org/debunked-first-object-teleported-to-earths-orbit-quantum-communication.t8908/

เรียบเรียง

สิขรินทร์ อยู่คง (QuTE Co-Founder)

วิทยาลัยเพื่อการค้นคว้าระดับรากฐาน (Institute for Fundamental Study: IF)

มหาวิทยาลัยนเรศวร

quantum entanglement, quantum monogamy, quantum teleportation

Site Default